牛顿法在数值计算中可以用来求解方程式,也可以在优化问题中求极值,分别对应下面两个例子~
牛顿迭代求解Sqrt问题
求解x=Sqrt(n),令,如下图所示:
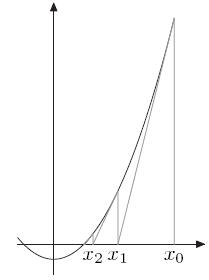
求得点的切线方程为:,其中
由于我们要求使的点,所以,令,得:
之后就可以通过上面迭代公式求解:
public int sqrt(int x){
double res = 1;
double last = 0;
while(res != last){
last = res;
res = (res + x/res)/2;
}
return (int)res;
}
参考:1
牛顿法求解优化问题
牛顿法求解优化问题的思路和上面求解一致,唯一不同的是优化问题中都是求最小(大)值,需要转化一下,考虑到极值点梯度为0,所以牛顿法就是通过求解梯度为0来解决优化问题的
考虑无约束优化问题:
假设具有连续二阶偏导数,第k次迭代值为,将在处进行二阶泰勒展开:
其中,点的梯度向量;点的海赛矩阵(Hesse matrix)
函数f(x)有极值的必要条件是在极值点处梯度向量为0,假如第k+1次的迭代值是极值的话,有:
对泰勒展开式求导得:,所以,最后得迭代公式为:
牛顿法就是根据上面的迭代公式求最优值的,一般求值曲线如下:
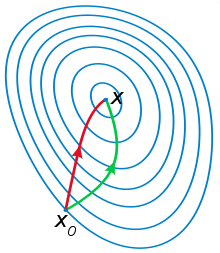
上图对比了梯度下降法(绿线)和牛顿法(红线)求解最小化问题的过程。梯度下降使用梯度(一阶导数)寻找下降最快的方向,而牛顿法通过曲率(二阶导数)寻找下降最快的方向,因此牛顿法的路径更直接。
从几何上说,牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面,通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径。
拟牛顿法
在牛顿法的迭代中,需要计算海赛矩阵的逆,计算复杂度很高,考虑使用一个n阶矩阵近似代替。这就是逆牛顿法的思路
Hesse矩阵在拟牛顿法中是不计算的,拟牛顿法是构造与Hesse矩阵相似的正定矩阵,这个构造方法,使用了目标函数的梯度(一阶导数)信息和两个点的“位移”(Xk-Xk-1)来实现。有人会说,是不是用Hesse矩阵的近似矩阵来代替Hesse矩阵,会导致求解效果变差呢?事实上,效果反而通常会变好。
拟牛顿法与牛顿法的迭代过程一样,仅仅是各个Hesse矩阵的求解方法不一样。
在远离极小值点处,Hesse矩阵一般不能保证正定,使得目标函数值不降反升。而拟牛顿法可以使目标函数值沿下降方向走下去,并且到了最后,在极小值点附近,可使构造出来的矩阵与Hesse矩阵“很像”了,这样,拟牛顿法也会具有牛顿法的二阶收敛性。
下面给出DFP法的求解过程:
上面我们对二阶泰勒公式求导得到:
当时:
可以推导出一组解为:
这样就得到了的迭代公式
[](http://www.cnblogs.com/zhangchaoyang/articles/2600491.html)