关于SVM入门的笔记，更多请参考这里。

基本介绍

支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的 根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度，Accuracy）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折衷，以期获得最好的推广能力（或称泛化能力）。

所谓VC维是对函数类的一种度量，可以简单的理解为问题的复杂程度，VC维越高，一个问题就越复杂。正是因为SVM关注的是VC维，后面我们可以看到，SVM解决问题的时候，和样本的维数是无关的（甚至样本是上万维的都可以，这使得SVM很适合用来解决文本分类的问题，当然，有这样的能力也因为引入了核函数）。

不是很理解VC维和这句话，我的理解是VC维和样本维度是相关的，比如样本维度是2，最多就有2^2个样本，如果是二分类问题，’最大的VC维‘就是2^(2^2) 如果相关的话，上面的话不是矛盾么？

统计学习因此而引入了泛化误差界的概念，就是指真实风险应该由两部分内容刻画，一是经验风险，代表了分类器在给定样本上的误差；二是置信风险，代表了我们在多大程度上可以信任分类器在未知文本上分类的结果。很显然，第二部分是没有办法精确计算的，因此只能给出一个估计的区间，也使得整个误差只能计算上界，而无法计算准确的值（所以叫做泛化误差界，而不叫泛化误差）。

置信风险与两个量有关，一是样本数量，显然给定的样本数量越大，我们的学习结果越有可能正确，此时置信风险越小；二是分类函数的VC维，显然VC维越大，推广能力越差，置信风险会变大。

统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小，即结构风险最小。

SVM正是这样一种努力最小化结构风险的算法。

小样本，并不是说样本的绝对数量少（实际上，对任何算法来说，更多的样本几乎总是能带来更好的效果），而是说与问题的复杂度比起来，SVM算法要求的样本数是相对比较少的。

非线性，是指SVM擅长应付样本数据线性不可分的情况，主要通过松弛变量（也有人叫惩罚变量）和核函数技术来实现，这一部分是SVM的精髓

高维模式识别是指样本维数很高，例如文本的向量表示，如果没有经过另一系列文章（《文本分类入门》）中提到过的降维处理，出现几万维的情况很正常，其他算法基本就没有能力应付了，SVM却可以，主要是因为SVM 产生的分类器很简洁，用到的样本信息很少（仅仅用到那些称之为“支持向量”的样本，此为后话），使得即使样本维数很高，也不会给存储和计算带来大麻烦（相对照而言，kNN算法在分类时就要用到所有样本，样本数巨大，每个样本维数再一高，这日子就没法过了……）。

有两个地方不理解：

1. ‘其他算法基本就没能力应付了’中其他算法出了后面提到的knn还有谁？粗略想了一下常见的分类算法，贝叶斯，决策树，线性回归，逻辑回归这些都OK吧？
2. ‘用到的样本信息很少’也不是理解

线性分类模型

二元的线性分类问题中，分类标记只有-1和1，分类面为：$g(x) = w * x + b = 0$， 这样，分类预测函数为一个符号函数： $$ sgn(x)= \left{\begin{matrix} 1 & if ~g(x)>0,\ -1 &else \end{matrix} \right. $$

样本点$x_i$ 对应分类 $y_i$ ，到分类面的函数距离为: $y_i * (w * x_i + b) = \mid g(x_i) \mid$

SVM使用的是样本点到分类面的几何距离(点到面的距离)：$\frac{1}{\mid w \mid} * \mid g(x_i)) \mid$

可见，几何距离 = 函数距离 / w

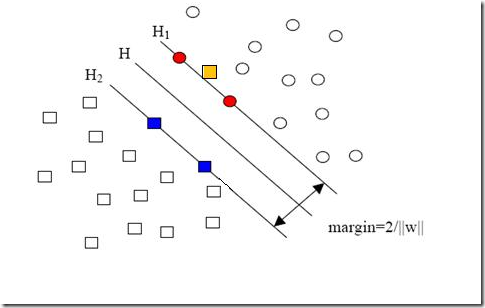
H是分类面，而H1和H2是平行于H，且过离H最近的两类样本的直线，H1与H，H2与H之间的距离就是几何间隔

几何间隔与样本的误分次数间存在关系: $\text{误分类个数} \leqslant ( \frac{2R}{\delta } )^{2}$

其中的δ是样本集合到分类面的间隔，$R= \max_{i=1}^n \mid x_i \mid$ 即R是所有样本中（xi是以向量表示的第i个样本）向量长度最长的值

现在可以设计最大化几何距离的线行分类器，SVM做的就是固定间隔，求最小的$\mid w \mid$

几何距离和$\mid w \mid$成反比，因此最大话几何距离，相当于最小化$\mid w \mid$，等价于最小化$\mid w \mid ^{2}$

因为我们实际上并不知道该怎么解一个带约束的优化问题。如果你仔细回忆一下高等数学的知识，会记得我们可以轻松的解一个不带任何约束的优化问题（实际上就是当年背得烂熟的函数求极值嘛，求导再找0点呗，谁不会啊？笑），我们甚至还会解一个只带等式约束的优化问题，也是背得烂熟的，求条件极值，记得么，通过添加拉格朗日乘子，构造拉格朗日函数，来把这个问题转化为无约束的优化问题云云（如果你一时没想通，我提醒一下，构造出的拉格朗日函数就是转化之后的问题形式，它显然没有带任何条件）。

样本确定了w，用数学的语言描述，就是w可以表示为样本的某种组合：$w = a_1x_1 + a_2x_2 +...+ a_nx_n$ α被称为拉格朗日乘子

不明白为什们w是x的线性组合函数？？

w不仅跟样本点的位置有关，还跟样本的类别有关（也就是和样本的“标签”有关）。因此用下面这个式子表示才算完整：$w=a_1y_1x_1 + a_2y_2x_2 +...+ a_ny_nx_n$

a可正可负，为什么还需要y呢？？

w可简写为：$w=\sum_{i=1}^{n} a_iy_ix_i$

g(x)为： $g(x)=<w,x>+b=<\sum_{i=1}^{n}a_iy_ix_i,x>+b=\sum_{i=1}^{n}a_iy_i<x_i, x>+b$

核函数

核函数的基本作用就是接受两个低维空间里的向量，能够计算出经过某个变换后在高维空间里的向量内积值。

只要是满足了Mercer条件的函数，都可以作为核函数。

这样，g(x)使用和函数K后形式为：$g(x)=\sum_{i=1}^{n}a_iy_iK(x_i, x)+b$

松弛变量

就是图中黄色那个点，它是方形的，因而它是负类的一个样本，这单独的一个样本，使得原本线性可分的问题变成了线性不可分的。这样类似的问题（仅有少数点线性不可分）叫做“近似线性可分”的问题。

为了减小噪音点对分类器的影响，添加松弛变量,原来的优化问题转化为：

• min: $1/2 \mid w \mid ^{2} + C\sum_{i=1}^{l}\zeta_i$
• subject to: $y_i (wx_i+b) >= 1-\zeta_i \\ (i=1,2,3..,l)(l样本数)(\zeta_i>=0)$

其中，C的大小表示对噪音点的重视，C越大，zata越小，被视为噪音的点越少

C因此经常被用来解决分类问题中的数据倾斜现象

先来说说样本的偏斜问题，也叫数据集偏斜（unbalanced），它指的是参与分类的两个类别（也可以指多个类别）样本数量差异很大。比如说正类有10，000个样本，而负类只给了100个

给样本数量少的类别赋予更大的惩罚银子C，表示越重视这些样本，将小这些样本被视为噪音点的概率